2025知到答案 概率论与数理统计(西安培华学院) 最新智慧树满分章节测试答案
第一章 单元测试
1、单选题:
甲乙二人进行射击A,B分别表示甲、乙击中目标,则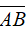 表示的事件是( ).
表示的事件是( ).
选项:
A:两人都没击中目标
B:至少有一人击中目标
C:两人都击中目标
D:至少有一人没击中目标
答案: 【至少有一人没击中目标】
2、判断题:
在某次抽奖活动中,参与者从一个包含100个不同号码的样本空间中随机抽取1个号码。假设每个号码被抽中的概率相等。若抽中的号码为偶数,则参与者可以获得额外的奖金。根据概率的定义,参与者抽中偶数号码的概率为0.5。这个说法是正确的还是错误的?
选项:
A:对
B:错
答案: 【错】
3、单选题:
在一次掷骰子的实验中,出现任何一个数字(1到6)都被称为随机事件。以下关于随机事件的描述中,哪一项是正确的?
选项:
A:随机事件是指在确定条件下必然发生的事件。
B:随机事件的结果是不可预测的,每次实验的结果可能不同。
C:随机事件是指每次实验结果都相同的事件。
D:随机事件只涉及到不确定性,不需要进行实验。
答案: 【随机事件的结果是不可预测的,每次实验的结果可能不同。】
4、单选题:
在一场投掷一枚公平的六面骰子的实验中,求掷出一个偶数的概率。根据古典概型的定义,掷出偶数的结果有哪些?
选项:
A:1, 3, 5
B:2, 3, 4, 5, 6
C:1, 2, 3, 4, 5, 6
D:2, 4, 6
答案: 【2, 4, 6】
5、单选题:
在一次医学研究中,研究人员对一种新药的效果进行分析。已知该药物对某种疾病的治愈率为70%,而在该疾病患者中,有40%的人还伴有其他健康问题。如果研究表明,服用该药物的患者中有60%的人在治疗后恢复健康,且这60%的患者中有50%的人没有其他健康问题。请问,该药物在没有其他健康问题的患者中的治愈率为多少?
选项:
A:50%
B:70%
C:35%
D:80%
答案: 【50%】
6、判断题:
若事件A和事件B是两个互不相干的事件,则事件A和事件B同时发生的概率可以用乘法公式计算,即P(A∩B) = P(A) × P(B)。此说法正确吗?
选项:
A:错
B:对
答案: 【对】
7、多选题:
条件概率是指在已知某事件发生的条件下,另一个事件发生的概率。以下哪些选项正确描述了条件概率的含义和计算方法?
选项:
A:如果事件 B 的概率为零,则条件概率无法计算。
B:条件概率可以用来评估事件之间的相关性。
C:
条件概率的计算公式为 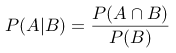 。
。
D:条件概率是指两个事件同时发生的概率。
答案: 【
如果事件 B 的概率为零,则条件概率无法计算。
;
条件概率可以用来评估事件之间的相关性。
;
条件概率的计算公式为 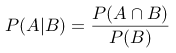 。
。
】
8、多选题:
在一次疾病检测中,研究人员发现某种疾病在普通人群中的发病率为1%。该检测的灵敏度为90%(即真正阳性的概率为0.9),特异度为95%(即真正阴性的概率为0.95)。如果一个人经过检测结果为阳性,使用贝叶斯公式计算该人实际患病的概率为多少。以下哪几项是正确的推论?
选项:
A:贝叶斯公式可以帮助我们更新对事件发生概率的认识。
B:即使检测为阳性,该人仍有可能是健康的,概率大约为10%。
C:检测结果为阳性时,实际患病的概率远高于1%。
D:灵敏度和特异度的高低对最终结果影响巨大。
答案: 【贝叶斯公式可以帮助我们更新对事件发生概率的认识。;
即使检测为阳性,该人仍有可能是健康的,概率大约为10%。;
检测结果为阳性时,实际患病的概率远高于1%。;
灵敏度和特异度的高低对最终结果影响巨大。】
9、单选题:
已知乘法公式为 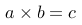 ,如果
,如果 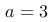 ,
,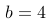 ,那么
,那么 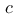 的值为多少?
的值为多少?
选项:
A:7
B:12
C:10
D:15
答案: 【12】
10、单选题:
在一次随机实验中,有两个事件A和B。如果已知事件A的发生与事件B的发生是独立的,那么根据条件概率的定义,以下哪一项是正确的?
选项:
A:P(A|B) = P(A) + P(B)
B:P(A|B) = P(A) * P(B)
C:P(A|B) = P(A)
D:P(A|B) = P(A) / P(B)
答案: 【P(A|B) = P(A)】
11、多选题:
关于随机事件的定义与性质,下列说法正确的是哪些?
选项:
A:随机事件的补事件是指在试验中不发生该事件的所有可能结果。
B:随机事件的概率值总是大于等于0且小于等于1。
C:每个随机事件都有确定的概率值。
D:随机事件是指在某个试验中可能发生的结果。
答案: 【随机事件的补事件是指在试验中不发生该事件的所有可能结果。;
随机事件的概率值总是大于等于0且小于等于1。;
随机事件是指在某个试验中可能发生的结果。】
12、多选题:
在一项市场调查中,研究人员发现两个产品A和B的购买行为之间存在某种关系。假设事件A表示选择产品A,事件B表示选择产品B。根据调查,消费者选择产品A和产品B的概率分别为P(A) = 0.4和P(B) = 0.5。同时,调查显示在选择产品A的消费者中,有60%的人也选择了产品B。请问以下哪些选项正确描述了事件A和事件B的关系?
选项:
A:根据给出的概率数据,我们可以计算出P(A∩B) = 0.4 × 0.5 = 0.2,进而得出事件A与事件B是独立事件。
B:事件A和事件B是独立事件,因为P(A)与P(B)的乘积等于P(A∩B)。
C:事件A和事件B不是独立事件,因为选择产品A的消费者中选择产品B的比例显示了它们之间的依赖关系。
D:如果事件A和事件B是独立事件,那么P(A∩B)应该等于P(A) × P(B)。
E:选择产品B的消费者中,选择产品A的概率可以帮助我们进一步分析这两个事件的依赖关系。
答案: 【事件A和事件B不是独立事件,因为选择产品A的消费者中选择产品B的比例显示了它们之间的依赖关系。;
如果事件A和事件B是独立事件,那么P(A∩B)应该等于P(A) × P(B)。;
选择产品B的消费者中,选择产品A的概率可以帮助我们进一步分析这两个事件的依赖关系。】
13、单选题:
在一场掷骰子的游戏中,掷出一个六面骰子的结果被称为随机事件。以下哪个选项最准确地描述了随机事件的含义?
选项:
A:随机事件是确定性事件,结果是可预测的。
B:随机事件是可以通过公式计算出结果的事件。
C:随机事件的结果总是相同的,不会变化。
D:随机事件是无法预测的事件,其结果只能通过实验或观察获得。
答案: 【随机事件是无法预测的事件,其结果只能通过实验或观察获得。】
14、单选题:
某学校共有100名学生,其中60名学生喜欢数学,45名学生喜欢英语,25名学生两门课都喜欢。请问随机抽取一名学生,他喜欢数学或英语的概率是多少?
选项:
A:0.45
B:0.60
C:0.75
D:0.80
答案: 【0.75】
15、单选题:
在一次科学实验中,研究人员需要分析两个不同事件之间的关系。事件A为“某种化学反应成功”,事件B为“实验室温度达到设定值”。已知这两个事件之间的关系不是互斥的,即事件A和事件B可以同时发生。请问在这种情况下,以下哪项描述最能准确反映事件A和事件B的关系?
选项:
A:事件A和事件B不具备任何相关性,它们的发生完全依赖于外部因素。
B:事件A和事件B互为独立事件,发生一个事件不会影响另一个事件的发生。
C:事件A的发生会影响事件B的发生,因此事件A和事件B是相关事件。
D:事件A和事件B是互斥事件,若事件A发生,则事件B必然不发生。
答案: 【事件A和事件B互为独立事件,发生一个事件不会影响另一个事件的发生。】
16、单选题:
在一次掷骰子的实验中,样本空间包含了所有可能的结果。根据样本空间的定义,掷出一个骰子时,样本空间是由以下哪些结果组成的?
选项:
A:1, 2, 3, 4, 5, 6, 7
B:1, 2, 3, 4, 5, 6
C:1, 2, 3
D:只有1
答案: 【1, 2, 3, 4, 5, 6】
17、单选题:
在随机事件中,如果事件 A 和事件 B 是两个互不相交的事件,那么事件 A 和事件 B 的并集的概率 P(A ∪ B) 可以用以下哪个公式表示?
选项:
A:P(A ∪ B) = P(A) × P(B)
B:P(A ∪ B) = P(A) - P(B)
C:P(A ∪ B) = P(A) / P(B)
D:P(A ∪ B) = P(A) + P(B)
答案: 【P(A ∪ B) = P(A) + P(B)】
18、单选题:
在一项调查中,研究人员发现某种疾病在特定人群中的发病率为0.1,而该人群中有70%的人曾经接触过某种风险因素。假设接触这种风险因素会增加该疾病的发病率到0.3。如果随机选取一个人,已知他接触过这种风险因素,求他患有该疾病的条件概率。
选项:
A:0.3
B:0.21
C:0.1
D:0.7
答案: 【0.21】
19、判断题:
在一次医学研究中,研究人员希望通过全概率公式计算特定疾病的发生概率。已知该疾病可以由三种不同的病因引起,而每种病因的发生概率和对应的条件概率均已知。研究人员认为,他们可以直接将每种病因的概率相加以得出该疾病的总体概率。请判断该研究人员的观点是否正确。
选项:
A:对
B:错
答案: 【错】
20、判断题:
贝叶斯公式可以用来计算在已知条件下事件发生的概率,因此,贝叶斯公式是条件概率的一种应用方法。
选项:
A:对
B:错
答案: 【对】
第二章 单元测试
1、单选题:
设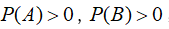 ,则A与B相互独立不能推出( )。
,则A与B相互独立不能推出( )。
选项:
A: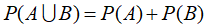
B: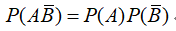
C: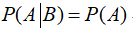
D: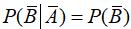
答案: 【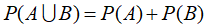 】
】
2、单选题:
在一项调查中,某公司发现每小时平均接到3个顾客的电话。若电话的接收符合“泊松分布”,那么在一个小时内接到5个电话的概率可以用哪个公式表示?
选项:
A:
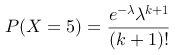 ,其中
,其中 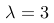 ,
, 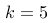
B:
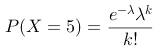 ,其中
,其中 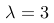 ,
, 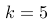
C:
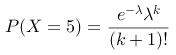 ,其中
,其中 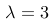 ,
, 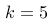
D:
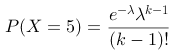 ,其中
,其中 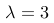 ,
, 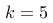
答案: 【
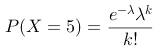 ,其中
,其中 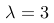 ,
, 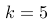
】
3、单选题:
在正态分布中,均值和方差分别对分布的图像特征有什么影响?以下哪项描述是正确的?
选项:
A:方差越大,分布的中心位置越偏离均值。
B:均值和方差都影响分布的中心位置。
C:均值和方差都决定了分布的形状,但与中心位置无关。
D:均值决定了分布的中心位置,方差决定了分布的宽度。
答案: 【均值决定了分布的中心位置,方差决定了分布的宽度。】
4、单选题:
在某个随机实验中,一个离散型随机变量 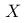 表示投掷一枚公平的六面骰子所得到的点数。现在定义一个新的随机变量
表示投掷一枚公平的六面骰子所得到的点数。现在定义一个新的随机变量 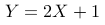 。请问,随机变量
。请问,随机变量 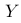 的期望值和方差分别为多少?并且在实际应用中,这种函数变换如何影响分布特征?
的期望值和方差分别为多少?并且在实际应用中,这种函数变换如何影响分布特征?
选项:
A:期望值为 7,方差为 5,函数变换使得分布中心上移,离散程度增加。
B:期望值为 8,方差为 4,函数变换使得分布中心上移,离散程度不变。
C:期望值为 6,方差为 6,函数变换使得分布中心不变,离散程度减小。
D:期望值为 9,方差为 9,函数变换使得分布中心下移,离散程度不变。
答案: 【期望值为 8,方差为 4,函数变换使得分布中心上移,离散程度不变。】
5、多选题:
关于连续型随机变量的分布特征,以下说法正确的是(可多选):
选项:
A:概率密度函数的积分值等于1。
B:分布函数可以取负值。
C:连续型随机变量的分布函数是非递减的。
D:概率密度函数在某一点的值可以大于1。
答案: 【概率密度函数的积分值等于1。;
连续型随机变量的分布函数是非递减的。】
6、多选题:
在一项研究中,科研人员考察了一个随机变量 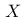 的分布情况,发现其服从正态分布
的分布情况,发现其服从正态分布 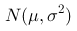 。他们希望通过随机变量
。他们希望通过随机变量 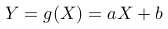 (其中
(其中 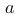 和
和 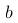 为常数)来研究
为常数)来研究 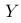 的分布特性。以下哪些选项正确描述了
的分布特性。以下哪些选项正确描述了 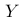 的分布特性?
的分布特性?
选项:
A:
可以通过变换函数 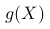 来计算
来计算 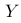 的累积分布函数。
的累积分布函数。
B:
若 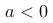 ,则
,则 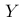 的分布会对称地反转。
的分布会对称地反转。
C:
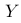 仍然服从正态分布,其均值为
仍然服从正态分布,其均值为  ,方差为
,方差为 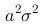 。
。
D:
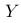 的分布形式会因常数
的分布形式会因常数 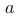 和
和 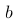 的不同而改变,因此不一定是正态分布。
的不同而改变,因此不一定是正态分布。
E:
若 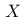 的分布为均匀分布,则
的分布为均匀分布,则 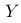 的分布也会是均匀分布。
的分布也会是均匀分布。
答案: 【
可以通过变换函数 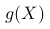 来计算
来计算 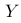 的累积分布函数。
的累积分布函数。
;
若 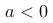 ,则
,则 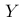 的分布会对称地反转。
的分布会对称地反转。
;
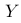 仍然服从正态分布,其均值为
仍然服从正态分布,其均值为  ,方差为
,方差为 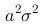 。
。
】
7、单选题:
对于一个离散随机变量 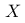 ,其概率分布为:
,其概率分布为: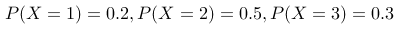 。请问该随机变量的期望值
。请问该随机变量的期望值 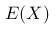 为多少?
为多少?
选项:
A:2.2
B:1.8
C:2.0
D:2.5
答案: 【2.0】
8、单选题:
在统计分析中,对于一个连续型随机变量 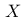 ,其均值为
,其均值为 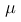 ,标准差为
,标准差为 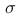 。如果我们对该随机变量进行标准化处理,得到新的随机变量
。如果我们对该随机变量进行标准化处理,得到新的随机变量 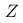 ,则
,则 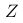 的计算公式为
的计算公式为 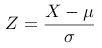 。请问,以下哪项描述最能反映标准化处理的目的?
。请问,以下哪项描述最能反映标准化处理的目的?
选项:
A:
标准化后的随机变量 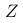 的均值为0,标准差为1,从而便于不同数据集的比较。
的均值为0,标准差为1,从而便于不同数据集的比较。
B:标准化处理可以提高随机变量的取值范围,使其更易于理解。
C:标准化处理可以消除随机变量的偏态分布,使其呈现正态分布。
D:标准化处理仅适用于正态分布的随机变量,其他分布无法进行标准化。
答案: 【
标准化后的随机变量 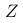 的均值为0,标准差为1,从而便于不同数据集的比较。
的均值为0,标准差为1,从而便于不同数据集的比较。
】
9、单选题:
在某个研究项目中,科学家试图分析两个随机变量 X 和 Y 的关系。研究发现,如果 X 和 Y 是独立的,则它们的联合分布可以表示为各自边际分布的乘积。假设 X 表示某城市的年降水量,而 Y 表示该城市的年温度。以下哪个选项最能说明在此研究中,X 和 Y 可能独立的实际意义?
选项:
A:X 和 Y 独立表明降水量和温度之间没有任何关系,因此可以忽略这些变量对生态系统的影响。
B:X 和 Y 独立说明在分析气候变化时,考虑一个变量的变化不会影响另一个变量的分析结果。
C:X 和 Y 独立意味着降水量的变化不会影响温度,因此可以预估未来气候变化的趋势。
D:X 和 Y 独立意味着降水量和温度的变化是随机的,无法通过任何模型进行预测。
答案: 【X 和 Y 独立说明在分析气候变化时,考虑一个变量的变化不会影响另一个变量的分析结果。】
10、判断题:
随机变量的期望值是其所有可能取值的加权平均,权重为相应取值的概率。因此,对于任何随机变量,期望值总是存在的。这个说法是正确的还是错误的?
选项:
A:对
B:错
答案: 【错】
11、判断题:
在某个城市的交通管理中,交通流量被建模为一个随机变量。研究发现,该随机变量的分布函数具有右连续性,并且在任意点处的左极限等于该点的函数值。此外,交通流量的分布函数在其定义域上是单调非降的。由此可以推断,该交通流量的分布函数在所有点上都是连续的。此判断是否正确?
选项:
A:对
B:错
答案: 【错】
12、单选题:
随机变量的定义中,哪一项描述是正确的?
选项:
A:随机变量的所有可能取值都是固定不变的。
B:随机变量是一个可以取任意值的变量。
C:随机变量只可以是离散的,不可以是连续的。
D:随机变量是一个与概率相关的函数,用于描述随机现象的结果。
答案: 【随机变量是一个与概率相关的函数,用于描述随机现象的结果。】
13、单选题:
在某个城市中,研究人员发现居民的年收入可以被视为一个随机变量 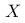 。他们通过分析数据得到了
。他们通过分析数据得到了 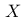 的分布函数
的分布函数  。根据这个分布函数,研究人员希望评估低收入群体的比例,即年收入低于
。根据这个分布函数,研究人员希望评估低收入群体的比例,即年收入低于 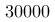 的居民所占的比例。假设
的居民所占的比例。假设 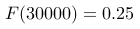 ,这意味着什么?在这个情况下,以下哪个选项最能正确解释这个结果?
,这意味着什么?在这个情况下,以下哪个选项最能正确解释这个结果?
选项:
A:25%的居民年收入低于30000,说明该城市的贫困率较高。
B:25%的居民年收入高于30000,说明城市中大部分人群经济状况较好。
C:75%的居民年收入低于30000,说明大部分居民收入较低。
D:收入为30000的居民所占比例为25%,说明收入分布均匀。
答案: 【25%的居民年收入低于30000,说明该城市的贫困率较高。】
14、多选题:
在一项调查中,研究人员希望分析某城市居民的收入水平。通过对1000名居民的收入数据进行收集和分析,研究人员发现收入分布可以近似为“正态分布”。根据这一特征,以下关于随机变量及其数字特征的描述中,哪些是正确的?
选项:
A:随机变量的方差可以反映数据的波动程度,方差越大,数据的波动越小。
B:如果收入是一个随机变量,二项分布适用于收入取值有限且每个居民的收入独立的情况。
C:正态分布的均值和中位数相等。
D:对于正态分布,方差越大,数据的分布越集中。
E:在正态分布中,约68%的数据落在均值的一个标准差范围内。
答案: 【如果收入是一个随机变量,二项分布适用于收入取值有限且每个居民的收入独立的情况。;
正态分布的均值和中位数相等。;
在正态分布中,约68%的数据落在均值的一个标准差范围内。】
15、多选题:
关于离散型随机变量的概率分布,下列说法中正确的有哪些?
选项:
A:离散型随机变量的期望值可以通过对每个可能取值乘以其概率求和得到。
B:二项分布和泊松分布是常见的离散型随机变量的概率分布。
C:所有离散型随机变量的概率分布都是均匀分布。
D:离散型随机变量的概率分布可以通过概率质量函数(PMF)来描述。
答案: 【离散型随机变量的期望值可以通过对每个可能取值乘以其概率求和得到。;
二项分布和泊松分布是常见的离散型随机变量的概率分布。;
离散型随机变量的概率分布可以通过概率质量函数(PMF)来描述。】
16、单选题:
在一次独立的试验中,某事件发生的概率为0.3,那么在进行5次试验中,事件恰好发生2次的概率可以用__________来计算。
选项:
A:几何分布
B:泊松分布
C:二项分布
D:正态分布
答案: 【二项分布】
17、单选题:
在某个城市的气象局,研究人员通过分析过去十年的气温数据,建立了一个关于气温的概率密度函数。已知该函数在区间 [0, 40] 的定义下,气温的概率密度函数为 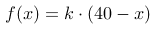 ,其中
,其中 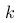 为常数。研究人员发现,气温低于 10 度的概率为 0.25。根据这些信息,以下哪项关于该概率密度函数的性质和应用的描述是正确的?
为常数。研究人员发现,气温低于 10 度的概率为 0.25。根据这些信息,以下哪项关于该概率密度函数的性质和应用的描述是正确的?
选项:
A:在气温达到 30 度时,概率密度函数的值为 0.5,因此气温越高,发生的概率越大。
B:由于该函数在区间 [0, 40] 的积分为 1,因此可以用于计算气温落在任意特定区间的概率。
C:该概率密度函数的均值大于 20 度,因此气温的平均水平较高。
D:
该概率密度函数是一个线性递减函数,其最大值出现在 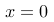 的位置。
的位置。
答案: 【由于该函数在区间 [0, 40] 的积分为 1,因此可以用于计算气温落在任意特定区间的概率。】
18、判断题:
连续型随机变量的概率密度函数的图像下方的面积等于1,这一说法是正确的吗?
选项:
A:对
B:错
答案: 【对】
19、单选题:
设有一连续型随机变量 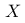 ,其概率密度函数为
,其概率密度函数为  ,定义在区间
,定义在区间 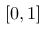 。请问,随机变量
。请问,随机变量 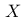 的分布函数
的分布函数 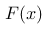 在
在 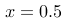 的值为多少?(提示:分布函数的计算需要对概率密度函数积分)
的值为多少?(提示:分布函数的计算需要对概率密度函数积分)
选项:
A:1
B:0.5
C:0.25
D:0.75
答案: 【0.75】
支付后可长期查看
有任何疑问及时添加客服QQ:2025479448反馈
网站只是章节,不包含期末
购买期末+QQ:2025479448
