2025知到答案 高等代数Ⅱ(河西学院) 最新智慧树满分章节测试答案
绪论 单元测试
1、判断题:
对于线性空间的学习,要从三个方面讨论:定义,线性关系(主要是在有限维空间中),子空间。
选项:
A:错
B:对
答案: 【对】
2、判断题:
对于线性空间中线性关系的研究有一个非常重要的概念,就是n维线性空间的基,有了基就可以把数域P上抽象的n维线性空间模型化成具体的空间Pn,而把抽象的向量模型化成它的坐标,即有序数组。
选项:
A:错
B:对
答案: 【对】
3、判断题:
对于线性空间的认识,不仅要知道线性空间的定义,还要了解基本性质以及认识一些具体的线性空间。
选项:
A:错
B:对
答案: 【对】
4、判断题:
线性空间立足于它的基础——集合,于是可以通过学习线性空间的子空间来更好的把握全空间,对于子空间的学习,需要把握其存在性、有限维空间中子空间的构造——生成子空间以及子空间的运算。
选项:
A:错
B:对
答案: 【对】
第一章 单元测试
1、判断题:
全体实对称矩阵关于矩阵的加法和数量乘法构成实数域上 维的线性空间。
选项:
A:错
B:对
答案: 【错】
2、判断题:
每一n维线性空间都可以表示成n个一维子空间的直和。
选项:
A:错
B:对
答案: 【对】
3、判断题:
数域P上两个有限维线性空间同构的充要条件是它们有相同的维数。
选项:
A:对
B:错
答案: 【对】
4、判断题:
在中,子集
构不成子空间。
选项:
A:错
B:对
答案: 【对】
5、单选题:
在中,向量
在基
,
,
,
下的坐标是( )。
选项:
A:(2,—1,1,0)
B:(1,0,0,2)
C:(—1,0,0,2)
D:(2,—1,0,0)
答案: 【(2,—1,0,0)】
6、单选题:
在数域P上的n维线性空间V中,由基到基
的过渡矩阵是A,由基
到基
的过渡矩阵是B。那么由基
到基
的过渡矩阵是( )。
选项:
A:
B:
C:
D:
答案: 【
】
7、单选题:
设![]() 是线性空间
是线性空间中三个互素的多项式,但其中任意两个都不互素。则
![]() ( )。
( )。
选项:
A:线性相关
B:是的一个基
C:最大公因式是一次多项式
D:线性无关
答案: 【线性无关】
8、多选题:
子空间的和是直和的充要条件是( )。
选项:
A:
⊂
B:
dimdim
+dim
C:
D:
答案: 【
dimdim
+dim
;
;
】
9、多选题:
下列说法正确的有( )。
选项:
A:实数域关于数的加法和乘法构成复数域上的线性空间
B:实数域关于数的加法和乘法构成自身上的线性空间
C:复数域关于数的加法和乘法构成有理数域上的线性空间
D:有理数域关于数的加法和乘法构成实数上的线性空间
答案: 【实数域关于数的加法和乘法构成自身上的线性空间;
复数域关于数的加法和乘法构成有理数域上的线性空间】
10、多选题:
在数域P上的线性空间V中,如果向量满足
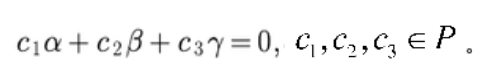 且
且。那么( )
选项:
A:
B:
线性无关
C:
dim
D:
线性相关
答案: 【
;
dim
;
线性相关
】
第二章 单元测试
1、判断题:
线性变换可对角化的充要条件是
有
个特征向量。
选项:
A:对
B:错
答案: 【错】
2、判断题:
设为
维线性空间
的一个线性变换,则由
的秩+
的零度
,有
![]() 。
。
选项:
A:对
B:错
答案: 【错】
3、单选题:
设定义
则下列向量中为
中的向量的是( ).
选项:
A:(4,-2,-2)
B:(-1,-2,1)
C:(-2,4,2)
D:(5,-2,-2)
答案: 【(-2,4,2)】
4、单选题:
设线性变换在基
下的矩阵为
,且
线性变换
在基
下的矩阵为
,则
( )。
选项:
A:
B:5
C:不能确定
D:
答案: 【不能确定】
5、多选题:
设为
维线性空间
上的一个线性变换,
是
的一组基且
在这组基下的矩阵为
,则 ( )。
选项:
A:
的值域是由基像和核生成的子空间
B:
的秩等于矩阵
的秩
C:
的值域是由基像生成的子空间
D:
的核的维数等于矩阵
的秩
答案: 【
的秩等于矩阵
的秩
;
的值域是由基像生成的子空间
】
6、判断题:
线性变换把线性无关向量组变成线性无关向量组。
选项:
A:错
B:对
答案: 【错】
选项:
A:错
B:对
答案: 【对】
8、单选题:
在多项式空间中,下列变换不是线性变换的是( )。
选项:
A:
B:
,
是P中的固定数。
C:
D:
答案: 【
】
9、单选题:
设级方阵
的每行元素之和为
,且
,则
的一个特征值为( )。
选项:
A:
B:
C:
D:
答案: 【】
10、单选题:
设,若矩阵
相似于
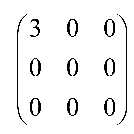 ,则
,则。
选项:
A:1
B:4
C:3
D:2
答案: 【2】
